| |
Н. Воробьев
Сумматоры: определения, классификация, уравнения, структуры и применение
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Сумматоры классифицируют по различным признакам.
В зависимости от системы счисления различают:
- двоичные;
- двоично-десятичные (в общем случае двоично-кодированные);
- десятичные;
- прочие (например, амплитудные).
По количеству одновременно обрабатываемых разрядов складываемых чисел:
- одноразрядные,
- многоразрядные.
По числу входов и выходов одноразрядных двоичных сумматоров:
- четвертьсумматоры (элементы “сумма по модулю 2”; элементы “исключающее ИЛИ”), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;
- полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд);
- полные одноразрядные двоичные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд).
По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:
- последовательные, в которых обработка чисел ведётся поочерёдно, разряд за разрядом на одном и том же оборудовании;
- параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:
- с последовательным переносом;
- с параллельным переносом;
- с групповой структурой;
- со специальной организацией цепей переноса.
Три первых структуры будут подробно рассмотрены в последующих статьях. Среди сумматоров со специальной организацией цепей переноса можно указать:
- сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней [1];
- сумматоры с двухпроводной передачей сигналов переноса [1, 2];
- сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза) [3];
- асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.
По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:
- комбинационный, выполняющий микрооперацию “S = A плюс B”, в котором результат выдаётся по мере его образования (это комбинационная схема в общепринятом смысле слова);
- сумматор с сохранением результата “S = A плюс B”;
- накапливающий, выполняющий микрооперацию “S = S плюс B”.
Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема).
Важнейшими параметрами сумматоров являются:
- разрядность;
- статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;
- динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:
- от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;
- от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;
- от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;
- от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.
Четвертьсумматор
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент “сумма по модулю 2” и элемент “исключающее ИЛИ”. Схема (рис. 1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу её отражает таблица истинности 1 (табл. 1), а соответствующее уравнение имеет вид
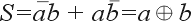 |
(1) |
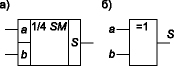
Рис. 1 |
Таблица 1
| a |
b |
S |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
Данный элемент выпускается в виде интегральных схем (ИС) типа ЛП5 (серии 133, 155, 530, 531, 533, 555, 1531, 1533); ЛП12 (555); ЛП107 (100, 500, 1500); ЛП2 (561, 564); ЛП14 (1561) и т. п.
Реализуем четвертьсумматор в базисах И-НЕ, ИЛИ-НЕ и с использованием только одного инвертора, для чего преобразуем уравнение (1):
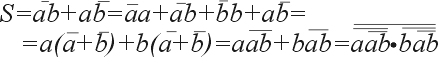 |
(2) |
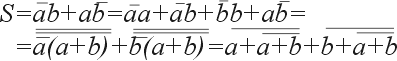 |
(3) |
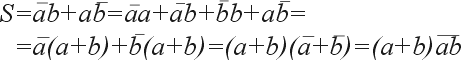 |
(4) |
Схемы, полученные по уравнениям (2)–(4), приведены на рис. 2.
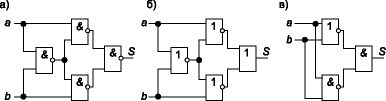
Рис. 2
Полусумматор
Полусумматор (рис. 3) имеет два входа a и b для двух слагаемых и два выхода: S — сумма, P — перенос. Обозначением полусумматора служат буквы HS (half sum — полусумма). Работу его отражает таблица истинности 2 (табл. 2), а соответствующие уравнения имеют вид:
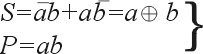 |
(5) |
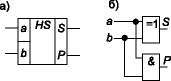
Рис. 3 |
Таблица 2
| a |
b |
P |
S |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
0 |
|
Из уравнений (5) следует, что для реализации полусумматора требуется один элемент “исключающее ИЛИ” и один двухвходовый вентиль И (рис. 3б).
Полный одноразрядный двоичный сумматор
Он (рис. 4) имеет три входа: a, b — для двух слагаемых и p — для переноса из предыдущего (более младшего) разряда и два выхода: S — сумма, P — перенос в следующий (более старший) разряд. Обозначением полного двоичного сумматора служат буквы SM. Работу его отражает таблица истинности 3 (табл. 3).
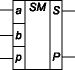
Рис. 4 |
Таблица 3
| № наб. |
a |
b |
p |
P |
S |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
1 |
| 2 |
0 |
1 |
0 |
0 |
1 |
| 3 |
0 |
1 |
1 |
1 |
0 |
| 4 |
1 |
0 |
0 |
0 |
1 |
| 5 |
1 |
0 |
1 |
1 |
0 |
| 6 |
1 |
1 |
0 |
1 |
0 |
| 7 |
1 |
1 |
1 |
1 |
1 |
|
Отметим два момента. Первый: в табл. 2 и 3 выходные сигналы P и S не случайно расположены именно в такой последовательности. Это подчеркивает, что PS рассматривается как двухразрядное двоичное число, например, 1 + 1 = 210 = 102 , то есть P = 1, а S = 0 или 1 + 1 + 1 = 310 = 112, то есть P = 1, а S = 1. Второй: выходные сигналы P и S полного двоичного сумматора относятся к классу самодвойственных функций алгебры логики. Самодвойственными называют функции, инвертирующие своё значение при инвертировании всех переменных, от которых они зависят. Обратите внимание, что P и S для четвертьсумматора и полусумматора не являются самодвойственными функциями! Преимущества, вытекающие из этого свойства полного двоичного сумматора, будут рассмотрены при анализе возможностей ИС типа 155ИМ1.
Уравнения, описывающие работу полного двоичного сумматора, представленные в совершенной дизъюнктивной нормальной форме (СДНФ), имеют вид:
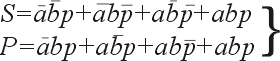 |
(6) |
Уравнение для переноса может быть минимизировано:
P = ab + ap + bp. (7)
При практическом проектированиии сумматора уравнения (6) и (7) могут быть преобразованы к виду, удобному для реализации на заданных логических элементах с некоторыми ограничениями (по числу логических входов и др.) и удовлетворяющему предъявляемым к сумматору требованиям по быстродействию.
Например, преобразуем уравнения (6) следующим образом:
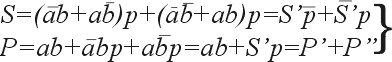 |
(8) |
Из выражений (8) следует, что полный двоичный сумматор может быть реализован на двух полусумматорах и одном двухвходовом элементе ИЛИ. Соответствующая схема приведена на рис. 5.
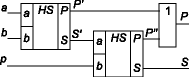
Рис. 5
Из выражения (8) для S также следует:
S = a Е b Е p. (9)
Примечание. Так как операция Е в выражении (9) коммутативна (переменные можно менять местами), то следует, что три входа полного двоичного сумматора абсолютно равноправны и на любой из них можно подавать любую входную переменную. Это полезно помнить, разводя печатные платы, на которых установлены ИС сумматоров.
К настоящему времени разработано большое число схем сумматоров. Доказано (нашим отечественным ученым Вайнштейном), что при использовании только одного инвертора нельзя реализовать полный двоичный сумматор со сложностью Pкв < 16, а при двух инверторах — Pкв < 14, где Pкв — вес по Квайну, используемый как оценка сложности любых комбинационных схем. Pкв — это общее число всех входов всех логических элементов схемы без учёта инверторов.
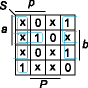
Рис. 6
Покажем, используя два метода, как была получена рациональная (с использованием только одного инвертора) схема полного двоичного сумматора, явившаяся основой схем ИС сумматоров типа 7480, 155ИМ1 и др.
Первый метод основан на использовании значения выходного переноса P как вспомогательной переменной при определении выходной суммы S (табл. 4). В табл. 4 при наборах переменных, являющихся нереальными (например, единичное значение переноса при нулевых значениях всех входных переменных), поставлены безразличные значения (крестик) для функции S, которые можно доопределять произвольным образом.
Таблица 4
| № наб. |
a |
b |
p |
P |
S |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
1 |
x |
| 2 |
0 |
0 |
1 |
0 |
1 |
| 3 |
0 |
0 |
1 |
1 |
x |
| 4 |
0 |
1 |
0 |
0 |
1 |
| 5 |
0 |
1 |
0 |
1 |
x |
| 6 |
0 |
1 |
1 |
0 |
x |
| 7 |
0 |
1 |
1 |
1 |
0 |
| 8 |
1 |
0 |
0 |
0 |
1 |
| 9 |
1 |
0 |
0 |
1 |
x |
| 10 |
1 |
0 |
1 |
0 |
x |
| 11 |
1 |
0 |
1 |
1 |
0 |
| 12 |
1 |
1 |
0 |
0 |
x |
| 13 |
1 |
1 |
0 |
1 |
0 |
| 14 |
1 |
1 |
1 |
0 |
x |
| 15 |
1 |
1 |
1 |
1 |
1 |
Из карты Карно для функции S (рис. 6) следует:
S = abp + Pa + Pb + Pp =
= abp + P(a + b + p). (10)
Второй метод основан на применении диаграмм Венна. На рис. 7а показана диаграмма Венна для трех переменных а, b, p; области, ограниченные окружностями, соответствуют переменным а, b, p, а области, обозначенные цифрами от 0 до 7 — соответствующим конъюнкциям (например, 5 = abp). Область, заштрихованная на рис. 7б, очевидно, соответствует функции P = ab + ap + bp. Функция S представлена заштрихованной областью на рис. 7в. Её можно представить суммой произведения функции a + b + p (рис. 7г) на функцию ab + ap + bp (рис. 7д) и функции abp (рис. 7е). Очевидно, что в этом случае получается выражение для S, аналогичное уравнению (10).
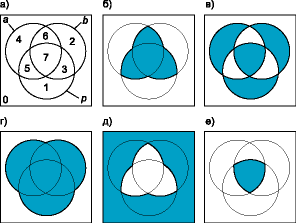
Рис. 7
Схема сумматора, реализованного по уравнениям (7) и (10), приведена на рис. 8а. В данной схеме используются многовходовые логические элементы И и ИЛИ. Если использовать только двухвходовые элементы, то получаются схемы, приведённые на рис. 8б,в.
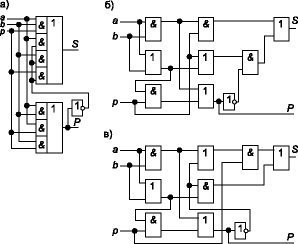
Рис. 8
Литература
- Самофалов К.Г., Корнейчук В.И., Тарасенко В.П. Электронные цифровые вычислительные машины: Учебник. — Киев: Высшая школа. — 1976. — 480 с.
- Потемкин И.С. Функциональные узлы цифровой автоматики. — М.: Энергоатомиздат. — 1988. — 320 с.
- Угрюмов Е.П. Проектирование элементов и узлов ЭВМ: Учеб. пособие для вузов. — М.: Высшая школа. — 1987. — 320 с.
Тел.: (095) 532 9955
|