В. Геппенер, А. Ланнэ, Д. Черниченко
МАТЛАБ для DSP. Использование GUI WAVEMENU для решения инженерных задач. Часть 1
Введение
Продолжая цикл статей “Matlab для DSP”, начатый в “Chip News” №2, 2000 г., эта статья посвящена использованию графического интерфейса пользователя (GUI) Wavemenu, при помощи которого можно получить удобный и наглядный доступ к основным процедурам toolbox Wavelet — наборе инструментов (коротко — тулбокс), встроенных в вычислительную среду MATLAB, для решения разнообразных инженерных задач, связанных с компрессией сигналов, анализом их особенностей, очисткой от шумов и др. В основе используемых процедур лежит относительно новая теория разложения сигналов по специальным функциям — всплескам (wavelet), главные особенности которых — ограниченность во времени, самоподобие и компактная локализация энергии по времени и частоте. Предполагается, что читатель знаком с основами этой теории [1,2,3,4].
Тулбокс Wavelet состоит из набора подпрограмм, которые позволяют:
- ознакомиться и исследовать характеристики индивидуальных wavelet и wavelet-пакетов;
- вычислять непрерывное wavelet-преобразование одномерных сигналов;
- производить анализ и синтез дискретных одномерных и двумерных сигналов на основе дискретного wavelet-преобразования;
- раскладывать одно- и двумерные сигналы по пакету wavelet;
- исследовать статистические характеристики сигналов;
- производить сжатие и очистку от шума одномерных и двумерных сигналов.
Использовать подпрограммы тулбокса Wavelet можно в режиме командной строки непосредственно из системы MATLAB. Это обычная практика для всех приложений пакета MATLAB. Применительно к обсуждаемому случаю предоставляется возможность решать широкий круг задач с помощью графического интерфейса — Wavemenu, который значительно облегчает применение основных подпрограмм тулбокса, а так же обеспечивает представление и визуализацию данных и результатов в удобной и наглядной форме.
Описание Wavemenu
Вызов Wavemenu
Wavemenu запускается из командной строки MATLAB командой “wavemenu”.
При вызове этой функции появляется главное меню GUI Wavemenu (рис. 1).
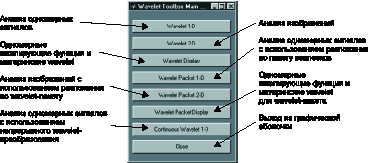
Рис. 1. Главное меню GUI Wavemenu
Структура Wavemenu
Wavemenu состоит из семи независимых разделов:
- Wavelet 1-D — предоставляет возможность анализа и синтеза одномерного сигнала с использованием дискретного wavelet-преобразования, сжатие сигнала и очистку его от шума;
- Wavelet 2-D — тоже для двумерных сигналов (например, изображений);
- Wavelet Display — даёт возможность посмотреть графики материнского wavelet и масштабирующей функции, соответствующие им коэффициенты КИХ-фильтров, а также получить краткую справку для каждого из используемых wavelet-семейств;
- Wavelet Packet 1-D — предоставляет возможность анализа и синтеза одномерного сигнала с использованием разложения по wavelet-пакету, сжатие сигнала и очистку его от шума;
- Wavelet Packet 2-D — то же для двумерных сигналов;
- Wavelet Packet Display — даёт возможность посмотреть графики материнского wavelet и масштабирующей функции wavelet-пакета, а также получить краткую справку по каждому из используемых wavelet-семейств;
- Continuous Wavelet 1-D предоставляет возможность анализа одномерного сигнала с использованием непрерывного wavelet-преобразования.
Меню для разделов Wavemenu
File Menu1 . Ниже описаны команды, поддерживающие работу GUI:
- Load Signal — загрузить сигнал, находящийся в MAT-файле [1], для его дальнейшего анализа в текущем разделе;
- Load Coefficients — загрузить коэффициенты wavelet-преобразования сигнала для дальнейшего анализа;
- Load Decompositions — загрузить декомпозицию сигнала;
- Save Synthesized Signal — сохранить в MAT-файле синтезированный сигнал;
- Save Coefficients — сохранить в MAT-файле коэффициенты wavelet-преобразования;
- Save Decompositions — сохранить декомпозицию сигнала;
- Demo Analysis — посмотреть примеры анализа демонстрационных сигналов;
- Print Settings — изменить текущие установки печати;
- Print — распечатать картинку с экрана, используя текущие установки печати;
- Close — выход из раздела Wavemenu и возврат к главному меню.
1 - некоторые пункты меню могут отсутствовать в различных разделах.
Options Menu служит для управления параметрами визуализации исходных данных и результатов анализа.
Экспорт и импорт информации из Wavemenu
Графический интерфейс позволяет импортировать информацию на диск и экспортировать информацию с жёсткого диска. Имеется возможность сохранения синтезированных сигналов, вычисленных wavelet-коэффициентов и декомпозиций на диске для дальнейшего использования в других приложениях или непосредственно в системе MATLAB. Напомним, что декомпозиция представляет собой часть сигнала, восстановленная по результату wavelet-разложения на некотором уровне.
Для сохранения синтезированного сигнала следует выбрать пункт меню “File->Save Synthesized Signal”. Появившийся диалог позволяет выбрать каталог и имя файла для сохраняемого сигнала. Имя переменной, содержащейся в получившемся MAT-файле, будет совпадать с именем файла.
Для сохранения wavelet-коэффициентов на диске, выбирается пункт меню “File->Save Coefficients”. Появится диалог, в котором можно задать каталог и имя файла для сохраняемого набора коэффициентов. Структура данных файла с wavelet-коэффициентами представлена в табл. 1 и на рис. 2. Для сохранения декомпозиции исходного сигнала используется пункт меню “File->Save Decompositions”. Структура данных файла с резуль- татами декомпозиции приведена в табл. 2.
Таблица 1
| Непрерывное Wavelet-преобразование (Continuous Wavelet 1-D) |
| Имя переменной |
Размер* |
Описание |
| coefs |
K x N |
Переменная "coefs" содержит коэффициенты непрерывного wavelet-преобразования |
| scales |
1 x K |
Переменная "scales" содержит значения масштабов |
| Дискретное Wavelet-преобразование (Wavelet 1-D) |
| Имя переменной |
Размер |
Описание |
| Coefs |
1 x M |
Переменная "coefs" содержит коэффициенты дискретного wavelet-преобразования |
| Longs |
1 x J |
longs - вектор, содержащий длины каждого из подвекторов |
*) К - число масштабов, по которым анализировался сигнал; N - длина исходного сигнала; J - количество уровней разложения для дискретного wavelet-преобразования; М - количество получившихся коэффициентов дискретного wavelet-преобразования.
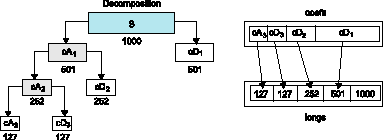
Рис. 2. Структура данных, содержащих коэффициенты wavelet-преобразования
Таблица 2
| Дискретное Wavelet-преобразование (Wavelet 1-D) |
| Имя переменной |
Размер* |
Описание |
| coefs |
1 x M |
Переменная "coefs" содержит коэффициенты дискретного wavelet-преобразования |
| data_name |
|
Строка, содержащая имя декомпозиции |
| longs |
1 x J |
longs - вектор, содержащий длины каждого из подвекторов |
| wave_name |
|
Строка, содержащая мнемоническое имя wavelet, использованного для декомпозиции |
| Разложение по wavelet-пакету (Wavelet Packet 1-D) |
| Имя переменной |
Размер |
Описание |
| data_name |
|
Строка, содержащая имя декомпозиции |
| data_struct |
|
Вектор, содержащий терминальные wavelet-коэффициенты |
| free_struct |
2 x P |
Матрица, содержащая структуру дерева wavelet-пакета |
*) J - количество уровней разложения для дискретного wavelet-преобразования; М - количество получившихся коэффициентов дискретного wavelet-преобразования; Р - количество терминальных узлов в дереве wavelet пакета (для полного дерева равно 2J+1).
В качестве загружаемых данных могут использоваться:
- тестовые сигналы, содержащиеся в каталоге MATLAB toolbox/wavelet/wavedemo;
- сигналы, сгенерированные любой программой, но обязательно в формате MAT-файла;
- сигналы, введённые извне в виде файла или с помощью звуковой карты и также представленные в формате MAT-файла.
Для представления произвольного сигнала в формате MAT-файла необходимо:
- загрузить сигнал в систему MATLAB (это можно сделать при помощи команд load или fscanf с соответствующими параметрами [5]);
- сохранить сигнал в MAT-файле (при помощи команды save), который имеет то же имя, что и переменная, содержащая сигнал (не более 8 символов).
Для загрузки wavelet-коэффициентов или декомпозиции сигнала необходимо придерживаться определённой структуры данных (табл. 1, 2 и рис. 2). Для загрузки данных в графический интерфейс используются пункты меню “File->Load Signal”, “File->Load Coefficients” или “File->Load Decompositions”, соответственно.
Использование Wavemenu для обработки сигналов
Едва ли не важнейшей при анализе и синтезе сигналов является идея представления сигнала в виде взвешенной суммы некоторых функций. Если эти функции обладают специальными свойствами, они называются базисами. Наиболее распространены в цифровой обработке сигналов базис единичных импульсов во временной области и базис, состоящий из экспонент, — в частотной. К сожалению, они не могут быть успешно использованы для представления нестационарных сигналов. Wavelet-преобразование позволяет разложить сигнал по компактным, хорошо локализованным по времени и частоте, базисным функциям (табл. 3), что позволяет, в отличие от преобразования Фурье, описывать нестационарные сигналы. При этом важно, что такое разложение достаточно экономно в вычислительном отношении.
Таблица 3
| Мнемоническое обозначение |
Название wavelet |
Характеристика соответствующего фильтра |
| Meyr |
Wavelet Мейера |
Фильтр с бесконечной гладкостью |
| Morl |
Wavelet Марлета |
Фильтр с бесконечным носителем |
| Mexh |
Wavelet "Мексиканская шляпа" |
| Haar |
Wavelet Хаара |
Ортогональные фильтра с конечной маской |
| DbN |
Wavelet Добеши |
| SymN |
"Симлеты" |
| CoifN |
"Койфлеты" |
| BiorNr, Nd |
Биортогональные wavelet |
Биортогональные фильтры с конечной маской |
В отличие от кратковременного преобразования Фурье (STFT), непрерывное wavelet-преобразование (CWT) имеет переменное разрешение по времени и частоте. В области высоких частот оно обеспечивает хорошее разрешение по времени и плохое по частоте, а в области низких частот — хорошее разрешение по частоте и плохое по времени (рис. 3). Применение wavelet-преобразования даёт хорошие результаты, особенно когда компоненты сигнала с высокой частотой имеют небольшую длительность, а низкочастотные компоненты — достаточно большую. Практически все биологические сигналы имеют подобную структуру.
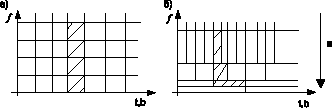
Рис. 3. Разбиение частотно-временного плана при STFT (a) и при CWT (б). При STFT окно анализа строго локализовано по времени и частоте, а при CWT локализация изменяется в зависимости от масштаба
Анализ с помощью непрерывного wavelet-преобразования выполняется примерно таким же образом, как и анализ с помощью кратковременного преобразования Фурье в том смысле, что сигнал умножается на некоторую функцию (wavelet), подобную окну в STFT. При этом ширина окна меняется по мере того, как вычисляется преобразование для каждой из компонент спектра.
Математическое определение непрерывного wavelet-преобразования [1-4]:
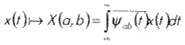
где x — сигнал, и yab — анализирующая функция. Для wavelet-преобразования анализирующая функция yab получается из одной базисной (или порождающей) функции y (mother wavelet)
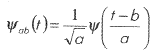
где a — параметр масштаба, который определяется как 1/частота, b — сдвиг по времени.
Функция y должна быть хорошо локализованной во временной и частотной областях и, кроме того, удовлетворять условию допустимости, гарантирующему существование обратного wavelet-преобразования.
Дискретное wavelet-преобразование наиболее эффективно в задачах сжатия сигналов и изображений, задаче очистки сигнала от шумов. Непрерывное wavelet-преобразование в основном используется для анализа переходных процессов, обнаружения резких изменений в сигнале и исследовании нестационарностей. Не так давно непрерывное wavelet-преобразование стало применяться в задаче распознавания образов: кривая в частотно-временной области трактуется как контур предмета.
Получение информации по конкретным wavelet
Основной при работе с wavelet-преобразованием является проблема выбора наиболее подходящего wavelet. Не существует каких-то жёстких правил, но лучше всего выбирать wavelet таким образом, чтобы он принадлежал такому же классу функций, что и анализируемый сигнал. Если исходную функцию можно аппроксимировать полиномом, то количество нулевых моментов wavelet должно примерно равняться степени полинома.
Числом нулевых моментов wavelet называется максимальное целое число P, при котором выполняется следующее равенство:
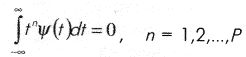
Другой важной проблемой является определение числа уровней разложения при дискретном wavelet-преобразовании. Так как на каждом уровне происходит октавное деление спектра (на полосы, отличающиеся в два раза), то количество уровней может быть вычислено исходя из наиболее низкочастотной компоненты сигнала, которая должна быть представлена в разложении.
Краткую информацию по каждому из wavelet можно получить в разделе “Wavelet Display” графического интерфейса. Для просмотра материнского wavelet, шкалирующей функции и коэффициентов связанных с ними КИХ-фильтров (если они существуют), следует выбрать пункт “Wavelet Display” в главном меню: появится следующая панель инструментов (рис. 4). Задавая тип wavelet при помощи кнопки “Display”, можно увидеть всю информацию о выбранном wavelet.
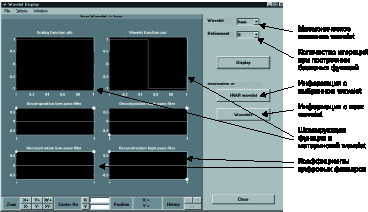
Рис. 4. Панель инструментов просмотра информации по wavelet
Основные характеристики [1-4]:
- скорость сходимости к 0 функций y, y и j, j, если время или частота стремятся к бесконечности. Скорость сходимости характеризует локализацию wavelet в частотной и временной областях;
- симметрия, необходимая для избежания фазовых искажений;
- число нулевых моментов y и j (если эти функции существуют);
- непрерывность.
Использование дискретного wavelet-преобразования
Дискретное wavelet-преобразование исключительно изящно и практически удобно представлять на основе теории цифровой фильтрации. Для этого используется два особым образом сконструированных КИХ-фильтра и прореживание по времени: сигнал пропускается через два фильтра — высокой и низкой частоты с передаточными функциями H(z) и G(z), соответственно, и одинаковой нормированной частотой среза, равной p/2. В результате фильтрации ширина спектра каждого сигнала на выходах фильтров уменьшается в два раза, и, соответственно, в два раза можно уменьшить частоту дискретизации высокочастотной и низкочастотной составляющих. Затем отсчёты высокочастотной составляющей, называемые wavelet-коэффициентами, запоминаются, а с низкочастотной составляющей происходит аналогичная операция. Это означает, что на каждом этапе происходит фильтрация низкочастотной составляющей, полученной на предыдущем этапе разложения, то есть разделение исходного спектра на две составляющие — низкочастотную и высокочастотную. Такая схема получила название схемы субполосного кодирования [1] (рис. 5).
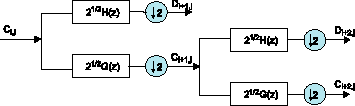
Рис. 5. Схема субполосного кодирования
Отсчёты сигналов на выходах фильтров с передаточными функ-циями H(z) и G(z) будут, соответственно, djk и cjk. Здесь индекс j — номер уровня, а k — момент времени. Сигналы djk и cjk вычисляются по формулам:
где {hj} и {gj} — импульсные характеристики фильтров.
Сложность вычисления дискретного wavelet-преобразования с помощью схемы субполосного кодирования линейна. Это означает, что число операций, необходимое для вычисления wavelet-разложения, линейно зависит от длины сигнала.
Так как КИХ-фильтры не являются идеальными, то происходит наложение спектров: в низкочастотную часть добавятся высокочастотные составляющие и наоборот. Однако фильтры построены таким образом, чтобы при последующем восстановлении этот эффект был скомпенсирован, и не происходило потери информации.
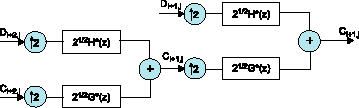
Рис. 6. Схема обратного преобразования
При обратном преобразовании (рис. 6) низкочастотная сj+2,k и высокочастотная dj+2,k составляющие дополняются нулями и пропускаются через КИХ-фильтры c передаточными функциями G*(z) и H*(z), однозначно определяемыми через G(z) и H(z). В результате получается низкочастотная составляющая cj+1,k и так далее [1]. Процедура заканчивается полным восстановлением исходного сигнала с.
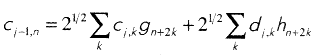
Для того, чтобы не происходило потери информации, коэффициенты {hj} и {gj} фильтров H(z) и G(z), соответственно, должны обладать следующими свойствами:
Изложенное выше иллюстрируется примером wavelet-преобразования сигнала, содержащимся в тестовом файле noischir.mat.
Этот сигнал имеет следующий вид:
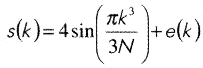
где N — продолжительность сигнала, в нашем случае, 1024 отсчёта; k = 1...N; e(k) — “белый” шум.
Для использования вышеупомянутого сигнала нужно выбрать пункт “Wavelet 1-D” в главном меню. Появится панель инструментов дискретного wavelet-анализа для одномерного сигнала (рис. 7). Для загрузки сигнала выбирается пункт меню “File->Load Signal”. Когда появится диалог загрузки сигнала, следует выбрать демонстрационный MAT-файл noischir.mat, который должен находиться в каталоге MATLAB toolbox/wavelet/wavedemo.
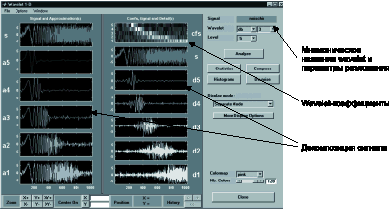
Рис. 7. Панель инструментов одномерного дисктерного wavelet-преобразования. В окне wavelet-коэффициентов светлому тону соответствуют коэффициенты с большим уровнем, а темному - с меньшим
После ввода сигнала произведём его разложение с использованием wavelet Добеши с 3-мя нулевыми моментами (‘db3’) до 5-го уровня. Максимальное число уровней ограничено длиной сигнала (в нашем случае, 1024 отсчёта). Результат разложения отображается двумерной картой. По оси ординат отложено время, а по оси абсцисс — уровень разложения (рис. 7). Более наглядно результат разложения можно оценить по декомпозиции сигнала {s1, d1, d2, d3, d4, d5}. Каждый элемент декомпозиции определяет вклад соответствующего уровня разложения (полосы частот) в исходный сигнал.
Очистка сигнала от шумов
Графический интерфейс позволяет решать задачи уменьшения уровня шума в дискретном (цифровом) сигнале (очистки от шума). Для этого необходимо нажать на кнопку “Denoise” в середине правой колонки, под кнопкой “Analyze”. Появится окно (рис. 8), в котором можно производить удаления шума из сигнала, используя дискретное wavelet-преобразование.
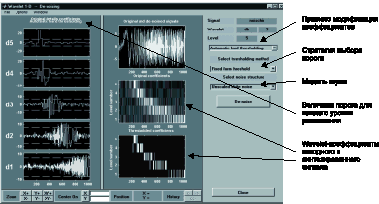
Рис. 8. Панель инструментов для очистки сигнала от шума при использовании одномерного дискретного wavelet-преобразования
Базовая модель сигнала с шумами имеет следующую форму:
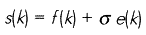
В самой простой модели предполагается, что e(k) — “белый” шум, где дисперсия s2 полагается равной 1.
Цель — подавление шумовой части сигнала s и восстановление функции f.
Процедура фильтрации шума производится в три этапа:
- Разложение сигнала. Выбирается тип wavelet и число уровней разложения J. Вычисляется wavelet-преобразование сигнала s до уровня J.
- Выбор порога для wavelet-коэффициентов. Для каждого уровня от 1 до J выбирается ej — порог, и производится модификация коэффициентов по определённому правилу (см. ниже).
- Восстановление сигнала. Производится обратное wavelet-преобразование с использованием модифицированных wavelet-коэффициентов.
Основные возникающие при этом вопросы относятся к выбору порога и правилу модификации коэффициентов.
Существуют два основных правила модификации wavelet-коэффициентов: “hard” и “soft” (рис. 9).
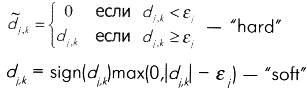
В GUI при очистке сигнала от шума необходимо задать следующие параметры: правило модификации wavelet-коэффициентов, правило выбора порога1 и модель шума.
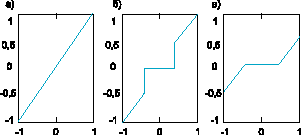
Рис. 9. Исходный сигнал (а); сигнал, модифицированный по правилу "hard" (б); сигнал, модифицированный по правилу "soft" (в)
Правила модификации wavelet-коэффициентов:
- Automatic soft thresholding — автоматический выбор порога, модификация коэффициентов по правилу “soft”;
- Automatic hard thresholding — автоматический выбор порога, модификация коэффициентов по правилу “hard”;
- Manual soft thresholding — ручной выбор порога, модификация коэффициентов по правилу “soft”;
- Manual hard thresholding — ручной выбор порога, модификация коэффициентов по правилу “hard”.
Правила выбора порога при автоматическом методе удаления шума:
- Fixed from threshold — фиксированный порог, равный sqrt(2*log(length(s)));
- Rigorous SURE — выбор, использующий квадратичную функцию потерь;
- Heuristic SURE — выбор, использующий комбинацию первых двух вариантов (при маленьком SNR используется фиксированный порог, при большом SNR — порог выбирается из оценки функции потерь);
- Minimax — выбор, использующий принцип минимакса (очищенный от шума сигнал аппроксимируется регрессионной моделью и выбирается порог, который реализует минимум максимальной среднеквадратичной ошибки, полученной для самой плохой функции в данном множестве).
Используемая модель шума:
- Unscaled white noise — “белый” шум;
- Scaled white noise — гауссовский шум, дисперсия шума s2 оценивается по самой высокочастотной составляющей сигнала — d1,k;
- Non-white noise — произвольный шум, дисперсия шума s2j вычисляется для каждого уровня разложения.
При ручном выборе порог может задаваться отдельно для каждого уровня wavelet-разложения.
В качестве примера рассмотрим очистку от шума сигнала
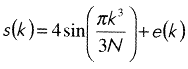
где N — продолжительность сигнала, в нашем случае, 1024 отсчёта; k = 1...N; e(k) — “белый” шум с дисперсией s2, равной 1.
Зададим автоматический выбор порога и модификацию wavelet-коэффициентов по правилу “hard” (Automatic hard thresholding), в качестве порога выберем фиксированный порог (Fixed from threshold) а в качестве модели шума примем “белый” шум (Unscaled white noise).
При нажатии на кнопку “De-noise” происходит очистка сигнала от шума в соответствии с заданными параметрами. Очищенный от шума сигнал накладывается на исходный. Так же строятся графики wavelet-коэффициентов исходного и очищенного (синтезированного) сигнала. При за-крытии окна инструмента удаления шума из сигнала (кнопка “Close”) появится диалог с вопросом “Обновить синтезированный сигнал?”, если нажать “Yes”, то синтезированный сигнал станет доступен в главном окне одномерного дискретного wavelet-анализа, где будет возможно проанализировать его статистические характеристики.
Сжатие сигнала
При сжатии сигнала используют следующую схему: производится wavelet-преобразование исходного сигнала, после чего запоминаются только значащие коэффициенты, то есть те, которые больше некоторого заданного порога. Восстановление сигнала производится при помощи обратного wavelet-преобразования, при этом пропущенные коэффициенты заменяются нулями.
Графический инструмент позволяет производить сжатие с автоматическим (Automatic thresholding) или ручным (Manual thresholding) выбором порога. В последнем случае порог для каждого уровня разложения можно задавать отдельно.
В качестве сигнала для сжатия будем использовать тот же сигнал
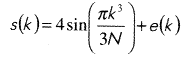
Для решения задачи сжатия сигнала следует вызвать соответствующий инструмент (рис. 10) нажатием кноп- ки “Compress”, размещённой в середине правой колонки окна, под кнопкой “Analyze”.
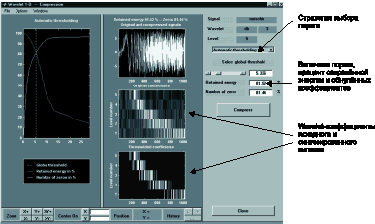
Рис. 10. Панель инструментов для сжатия сигнала при использовании одномерного дискретного wavelet-преобразования
При автоматическом выборе порога на самом левом графике отображаются процент сохранённой энергии сигнала и процент нулевых коэффициентов в зависимости от порога (вертикальная пунктирная линия).
Зададим автоматический выбор порога (automatic thresholding). Значением порога по умолчанию будет число, при котором процент сохранённой энергии сигнала будет равен проценту нулевых коэффициентов, в нашем случае, этот порог будет равен 5,326.
Если нажать кнопку “Compress”, то после паузы для вычисления исходный сигнал будет показан красным, а сжатый сигнал — жёлтым цветом.
Легко видеть, что в процессе сжатия сигнала мы удалили большинство коэффициентов (81,44%), сохранив в оставшихся 81,52% энергии сигнала.
При закрытии окна инструмента для сжатия сигнала (кнопка “Close”) опять появится диалог с вопросом об обновлении синтезированного (сжатого) сигнала.
Литература
- Strang G., Nguyen T. Wavelets and Filters Banks. — Wellesley-Cambridge-Press 1996. — 490 p.
- Daubechies Ingrid, Ten lectures on wavelets, SIAM, Philadelphia, 1992.
- Петухов А.П. Введение в теорию базисов всплесков. — СПб.: Изд-во СПбГТУ. — 1999. — 132 с.
- Michel Misiti, Yves Misiti, Georges Oppenheim, Jean-Michel Poggi. Wavelet Toolbox for use with Matlab (User’s Guide, version 1). — 626 p.
- Потемкин В.Г. MATLAB 5 для студентов /Диалог-МИФИ. — 1999. — 447 с.
arturlan@robotek.ru
|