А. Щука, С. Щука

Этапы развития технологии информации: от битов к кубитам

В современном обществе информация имеет решающее значение.На первоначальном этапе развития человеческой цивилизации основной категорией являлась материя и всё, что связанно с добычей материальных ценностей, переработкой сырья, использованием различных материалов для создания орудий труда. Вспомним каменный век, бронзовый… С ростом объёмов добычи и переработки сырья и материалов резко возросли потребности в энергии. Энергия как философская категория стала весьма значимой. ХХ век даже именовался веком атома, с атомной энергией связывают будущее человечества.А вот новый ХХI век уже претендует на признание его веком всеобщей информатизации общества. Информационные процессы характерны для искусства, науки, коммерческой деятельности и других сфер деятельности человеческого общества.

Понятие "информация" (от лат. informatio - разъяснение, изложение) - изначально обозначало сведения, передаваемые людьми устным, письменным или другими способами, с помощью условных сигналов и различных технических средств [1]. В научных исследованиях информация определяется как продукт взаимодействия данных и адекватных им методов, как диалектическое единство данных и методов в информационном процессе. Под информацией понимают также обмен сведениями как между людьми, так и между человеком и автоматом, автоматом и автоматом, обмен сигналами между животными и растениями, передачу признаков от клетки к клетке, от организма к организму.

Это весьма ёмкое понятие, объять которое невозможно. Остановимся на некоторых аспектах, имеющих отношение к электронным методам обработки и хранения информации. К сожалению, пока нет единой концепции понимания информации в рамках теории связи, теории систем, вычислительной техники, биологии, семиотики, лингвистики, теории коммуникаций и других направлениях исследований. Более того, возникают трудности в понимании меры информации, соотношения единиц информации в различных областях знаний, связи единицы информации с энергией и другими физическими величинами [2,3,4].

Целью настоящей работы является обзор методов обработки и хранения информации с помощью электронных средств вычислительной техники.

Схемотехнические методы обработки информации

В 1910 году физик П. Эренфест, работая в России, указал на возможность применения логики высказываний для описания переключательных цепей в телефонии. Он также разработал вычислительную машину, в качестве элементной базы которой были использованы телефонные реле с двумя состояниями "открыто/закрыто".

Затем появились работы американского учёного К. Шеннона, который трактовал информацию как послание, которое уменьшает неопределённость.

Шеннон первым показал, что информация может быть преобразована из одной формы в другую. В соответствии с теоремой Шеннона, для большого объёма информации существует двоичный код для передачи информации со сколь угодно малой вероятностью ошибки. Правильный алгоритм обработки информации позволяет отказаться от создания дорогостоящих каналов связи с низким уровнем помех.

Другими словами, была введена мера информации, основанная на двоичной системе счисления - бит.

Далее пошли исследования советских учёных В.И. Шестакова и А.Н. Колмогорова о применении математической логики в цифровой технике, работы Н. Винера и Дж. Фон-Неймана, заложившие основу кибернетики и современной вычислительной техники [3,4].

Введение двоичной меры информации позволило снять с полки запылившиеся от времени труды Джорджа Буля. В своей книге "Законы мысли" он изложил систему формальных обозначений и правил, близкой к математической логике. Правила этой системы универсальны и применимы к разным объектам и их группам. Результатом формального расчёта логического выражения является одна из двух сущностей - "Истина" и "Ложь". Четыре основные операции: "И" (пересечение), "ИЛИ" (объединение), "НЕ" (обращение) и "Исключающее ИЛИ" - сегодня лежат в основе всех цифровых устройств.

Элементной базой средств электронной вычислительной техники явились пассивные и активные электронные компоненты. Сначала это были телефонные реле, затем электронные лампы, на основе которых были созданы вычислительные машины первого поколения. С появлением дискретных транзисторов появились вычислительные машины второго поколения.

Во всех этих схемах бит информации отождествляется с появлением на выходе напряжения U¹, соответствующего логической единице или U⁰, соответствующего логическому нулю. В ряде электронных схем бит информации отождествляется с появлением заряда или тока в соответствующем месте схемы.

Революционным этапом развития средств вычислительной техники стало появление интегральных транзисторных структур. На базе этих структур стало возможным формировать активные и пассивные компоненты, интегрировать их на одном кристалле и создавать вычислительные структуры различного функционального назначения.

Следует особо подчеркнуть, что эти схемы обрабатывают дискретные сигналы, представляемые в двоичном виде. Именно схемы призваны обрабатывать и хранить информационные сигналы. Разработанная элементная база позволила создать различные вычислительные устройства, компьютеры различного уровня от микро- до супер- ЭВМ.

Однако, все они имели классическую архитектуру, предложенную ещё Фон-Нейманом (xрис. 1). Архитектура несколько менялась, в зависимости от вкусов разработчиков, но стержнем всех видов архитектур был процесс последовательного обмена информационными потоками от процессора к памяти и обратно. Несмотря на то, что в настоящее время достигнуто быстродействие около 109 операций в секунду, такая схема всё же является непреодолимым препятствием для дальнейшего роста производительности вычислительных устройств.

Рисунок 1. Фон-Неймановская вычислительная структура

Быстродействие микропроцессоров (время выполнения программы Т) определяется произведением количества команд программы (N) на среднее число машинных тактов на команду (I) и на длительность основного такта (C):

T = NxIxC.

Длительность одного такта, определяемая быстродействием транзисторных структур, в этой формуле не является определяющим фактором. Быстродействие элементной базы пока ещё удовлетворяет разработчиков.

Программисты максимально используют возможности архитектуры, с тем чтобы уменьшить количество команд. А вот последовательная перекачка информационных потоков в запоминающее устройство и обратно, определяемая фон-неймановской архитектурой, является сегодня сдерживающим фактором увеличения быстродействия.

Что касается создателей элементной базы, то в настоящее время предложены новые типы транзисторных структур, позволяющие достичь быстродействия переключения 10-11–10-12 с и частот свыше 200 ГГц. Это прежде всего транзисторы с проницаемой базой, гетеротранзисторы на основе GaAs и AlGaAs, транзисторы с планарно-легированными барьерами и транзисторы на баллистических электронах. На подходе транзисторы, использующие волновые свойства электронов и свехпроводниковые транзисторы [5].

Большие надежды возлагаются на транзисторные структуры, созданные по наноэлектронной технологии. Особый интерес у разработчиков суперкомпьютеров вызывают приборы, в которых используется перемещение определённого количества электронов и, в частности, одиночных электронов [6]. Создание одноэлектронных приборов открывает новые перспективы в системах цифровой обработки информации, в которых один бит информации будет представлен одним электроном.

Приборы этого класса работают на явлении туннелирования электронов, и поэтому предел быстродействия одноэлектронных приборов очень высок, частотный диапазон приборов на их основе составляет сотни терагерц. Энергопотребление этих приборов ожидается на уровне 10-8 Вт.

На рис. 2 приведена схема одноэлектронного транзистора. На поликремниевый слой наносится толстый слой диоксида кремния. С помощью процессов электронной литографии и ионного травления формируется островок Si-SiO2. На боковой поверхности островка с помощью термического окисления формируется тонкий слой окисла. Проводящие контакты формируются на основе поликремния.

Рисунок 2. Одноэлектронный транзистор

Разработаны приборы на многотуннельных переходах (Multi Tunnel Junctions - MTJ) [7].

Новые разработки и промышленное внедрение новых транзисторных структур может вообще снять вопрос об элементной базе современных средств вычислительной техники.

Однако вопрос об архитектуре компьютера далёк от своего решения. Стержневой идеей всех архитектур вычислительных устройств является предельное распараллеливание потоков обрабатываемого информационного массива. На быстродействии сказывается использование и отработанных стандартных подпрограмм.

Один из примеров - нейрокомпьютеры [8]. Элементами нейрологики являются нейроны. Каждый нейрон характеризуется своим текущим состоянием. К нейрону подходит группа межсоединений, именуемых синапсами. Это однонаправленные входные связи, соединённые с выходами других нейронов. Выходом нейрона является аксон. Каждый нейрон характеризуется величиной синаптической связи или её весом, эквивалентными электрической проводимости. Текущее состояние нейрона определяется как взвешенная сумма его входов. На аксоне формируется выходная функция состояния, которая называется активационной. Высокий параллелизм обработки достигается путём объединения большого числа нейронов в слои и оптимальным их межсоединением. Такая структура называется персептроном. К сожалению, в настоящее время для принципиально нового подхода к архитектуре вычислительных средств не разработана своя элементная база. Нейрокомпьютеры, как правило, реализуются на стандартных интегральных схемах, разработанных для совершенно других архитектур. Рассмотренные системы обработки информации основаны на обработке дискретных сигналов, заданных в двоичном коде. Во всех этих системах используются схемотехнические методы обработки информации. Между тем, по мнению множества экспертов, в том числе, самого Билла Гейтса, в ближайшее десятилетие может наступить эра нейрокомпьютеров. Может, это будут оптические нейрокомпьютеры [9]?

Несхемотехнические методы обработки информации

Параллельно идут поиски несхемотехнических методов обработки и хранения больших массивов информации.

Анализ схем цифровой обработки изображений показывает, например, что их быстродействие близко к предельным значениям. При этом ряд технических и вычислительных задач принципиально не может быть решён в рамках схемотехнических методов обработки больших информационных массивов.

Даже достигнув предельных значений быстродействия и степени интеграции в изделиях микроэлектроники, нельзя будет на их основе создать устройства, способные решить перспективные информационные задачи.

В этом случае возникает альтернатива: или искать пути сохранения тенденции экспоненциального роста степени интеграции ИС, или искать принципиально новый подход.

Можно ли удержать тенденцию экспоненциального роста степени интеграции микроэлектронных схем и, соответственно, экспоненциальное снижение стоимости обработки информации? Разработчики ИС активно ищут способы преодоления "тирании межсоединений", пути обхода технологических и физических барьеров на пути развития схемотехнической электроники. С этой целью разрабатываются вертикальные структуры, в которых стараются разместить максимум элементов на минимальной площади. Активные и пассивные элементы схемы размещаются в объёме, и интегральная схема становится трёхмерной. Как показали исследования, технология "кремний на диэлектрике" открывает определённые перспективы вертикальной интеграции, позволяет получать многоярусные транзисторные структуры. Предполагается, что трёхмерные ИС будут иметь высокое быстродействие, высокую плотность упаковки элементов, обладать возможностью параллельной обработки информации и станут многофункциональными. Но придётся преодолеть много препятствий, прежде чем в трёхмерных ИС удастся решить проблему взаимных помех элементов, разработать методы проектирования схем с комплексными параметрами и сложной топологией, сделать их конкуренто-способными по цене. Следует также отметить, что переход в трёхмерную электронику отнюдь не решает проблемы межсоединений, напротив, резко усложняет межуровневые соединения. Надёжность таких схем вызывает сомнение, доказательств обратного пока нет. Переход в трёхмерную электронику сулит только удвоение степени интеграции, а не её экспоненциальный рост в соответствии с законом Мура.

Могут ли "спасти" схемотехническую электронику метод интеграции на пластине или создание "суперкристаллов"? Проблема межсоединений в этих случаях принципиально тоже не решается, а значит и достижение успеха сомнительно. По этой же причине сомнительны перспективы использования в схемотехнической электронике различных эффективных и сверхминиатюрных транзисторных структур.

Можно ли уйти от проблемы "ирании межсоединений"? Видимо можно, но для этого нужно уйти от традиционного принципа обработки информации, отказаться от схемотехнической ячейки как основного преобразователя и хранителя информации.

Традиционная схемотехническая ячейка, будь то логическая ячейка или ячейка памяти, состоит из большого количества статических неоднородностей. Под статической неоднородностью понимается локальная область на поверхности или в объёме среды с отличными от её окружения свойствами, которая создаётся в результате строго определённых технологических процессов. Состояние таких статических неоднородностей позволяет генерировать, управлять или хранить информацию. Это и есть схемотехническая микроэлектроника, или электроника статических неоднородностей. В этом случае устройства обработки и хранения информации реализуются на определённых схемотехнических решениях.

В конце семидесятых годов возникла идея использовать динамические неоднородности в процессах обработки и хранения информации, а также физические принципы интеграции не только числа элементов, но и числа функций, выполняемых микроэлектронным прибором.

Идея использования динамической неоднородности в качестве носителя информации привела к формированию альтернативного пути в развитии микроэлектроники - функциональной электронике [10].

Динамическая неоднородность представляет собой локальный объём на поверхности или внутри среды с отличными от её окружения свойствами, она не имеет внутри себя статических неоднородностей и генерируется в результате определённых физико-химических процессов. Динамическая неоднородность может быть локализована или перемещаться по рабочему объёму континуальной среды в результате взаимодействия с различными физическими полями или динамическими неоднородностями такой же или другой физической природы. В процессе перемещения динамической неоднородности может происходить, например, перенос битов информации. Деградация динамической неоднородности не приводит, как правило, к потерям и сбоям в процессах обработки информации.

Известно большое количество динамических неоднородностей различной физической природы, факт наличия которых или их форма идентифицируется с битом информации. Это - ансамбли заряженных частиц и квазичастиц (зарядовые пакеты, флуксоны и т.п.), домены (электрические домены, домены Ганна, цилиндрические магнитные домены и т.п.), динамические неоднородности волновой природы (поверхностные акустические волны, магнитные статические волны) и т.п.

Идея использования динамических неоднородностей в приборах обработки и хранения информации является основополагающей, её развитие привело к становлению функциональной электроники. Это не схемотехническое направление в микроэлектронике, использующее в качестве носителей информации динамические неоднородности, основной тенденцией развития которого является интеграция функциональных возможностей приборов и устройств.

Приборы и устройства функциональной электроники могут быть использованы как для цифровой обработки информационных массивов, так и для аналоговой их обработки с выводом результатов в цифровой форме.

На рис. 3 приведены примеры использования некоторых устройств функциональной электроники для реализации известных логических операций, полностью дублирующих работу цифровых схемотехнических устройств. Но не это главное. Интегральные схемы эти операции выполняют лучше.

Рисунок 3. Логические элементы, реализованные на приборах с зарядовой связью (а, б) и на структурах с цилиндрическими магнитными доменами (в, г)

Замечательным свойством приборов функциональной электроники является использование в процессах обработки информации элементарных функций высшего порядка. К элементарным функциям высшего порядка отнесём: Фурье-преобразование; операцию свёртки; операцию корреляции; автокорреляцию; управляемую задержку информационного сигнала; хранение информации, в том числе, в виде многобитовых массивов; фильтрацию информационного сигнала; когерентное сложение сигналов; ответвление информационных сигналов; комбинированную обработку; информационных сигналов и так далее.

В то же время, в изделиях функциональной электроники элементарные функции высшего порядка могут быть реализованы наряду с традиционными элементарными функциями типа И, ИЛИ, НЕ и их различными комбинациями.

В функциональной электронике пока не существует принципиальных ограничений, связанных с размерами статиче-ских или динамических неоднородностей. Сравним изделия традиционной схемотехнической и функциональной электроники по быстродействию. В изделиях схемотехнической электроники перенос информационного сигнала происходит по линиям межсоединений, что снижает помехоустойчивость и надёжность изделий. В изделиях функциональной электроники массив информационных сигналов может быть обработан весь, целиком, не обязательно в виде отдельных битов информации. Возможно создание устройства, позволяющего производить обработку информации в аналоговом и цифровом видах одновременно, поэтому в устройствах обработки информации это позволит достичь производительности более 1015 операций/с.

В задачах обработки больших массивов информации определённые надежды связывают, например, с акустооптическими линейно алгебраическими процессорами, предназначенными для перемножения матрицы на вектор, матрицы на матрицу, тройного перемножения матриц и т.п. В таких процессорах используются свойства акустооптических ячеек: возможность модуляции интенсивности дифрагированного пучка и его отклонения на угол, пропорциональный частоте акустических колебаний в ячейке (рис. 4).

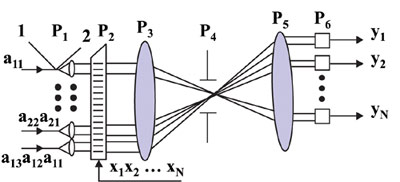
Рисунок 4. Схема акустооптического алгебраического процессора, реализованного на линзе

Элементы матрицы, соответствующим образом представленные сигналами a_ij, подаются на линейку источника света (1) в плоскости P1, их коллимированное излучение - на модулятор (3). Одновременно на модулятор подаются импульсы x₁, x₂,...,x_N, пропорциональные N-мерному вектору N. Результатом перемножения является вектор y = Ax, компоненты которого вычисляются по правилу:

i,j = 1...N.

Оптическая система из линз (4, 6) и диафрагмы (5) проецирует результат на линейку фотодетекторов (7). Работа устройства синхронизирована так, что в момент времени входа в апертуру ячейки первого акустического импульса первый источник света (фотодиод) излучает световой импульс с заданной интенсивностью a₁₁, а на выходе первого детектора появляется импульс тока, пропорциональный a₁₁·x₁. Следующий такт вычисления произойдёт, когда первый импульс сместится и будет направлен против второго светодиода, излучающего со световой интенсивностью, пропорциональной a₂₁.

В результате, суммарный выходной сигнал первого фотодетектора пропорционален a₁₁·x₁ + a₁₂·x₂. Через N таких тактов все элементы вектора x заполнят амплитуду ячейки, и величина сигнала нагрузки на i-том фотодетекторе будет пропорциональна

Теоретический предел скорости обработки составит (5 – 10)¹⁰ операций умножения/сложения в секунду. Аналогично строится процессор для перемножения матрицы на матрицу.

Ясно, что при обработке информационных массивов методами функциональной электроники оказывается эффективным использование аналоговых методов обработки и сопряжение их с цифровыми.

Одним из перспективных способов аналоговой обработки информации являются голографические методы, использующие интерференцию световых волн. Если две когерентные световые волны различной амплитуды распространяются в одном направлении, то в каждый момент времени происходит интерференционное сложение их амплитуд.

Регистрирующая среда, например, фотопластинка или другой какой-либо квадратичный детектор зафиксирует распределение интенсивности этой волны.

На языке функциональной электроники такие максимумы электрического поля интерферирующих волн представляют собой динамические неоднородности. Действительно, это локальные объёмы в достаточно однородной среде, создаваемые в результате обратимых физических процессов.

Динамическая неоднородность в виде максимума интенсивности световой волны способна переносить информационный сигнал и является кратковременной.

Отметим некоторые особенности.

1. Интересным свойством таких динамических неоднородностей является их способность быть "замороженной" в регистрирующей среде. Например, в фотопластинке такие динамические неоднородности замораживаются в виде сильно деформированных интерференционных полос (рис. 5).

   
   Рисунок 5. Голограмма представляет собой дифракционную структуру, наложенную на интерференционную и образующую совокупность "замороженных" сгустков интенсивностей электромагнитных волн

   Если такую фотопластинку поместить на пути когерентного пучка света, то происходит "разморозка" динамических не-однородностей и восстанавливаемая световая волна имеет распределение динамических неоднородностей, тождественное ранее записанному на фотопластинке.

2. И ещё одно замечательное свойство такого типа динамических неоднородностей, возникающих в процессе интерференции двух или более световых волн. Микроструктура записанных в среде динамических неоднородностей представляет собой электромагнитное поле модуляции амплитудой и фазой несущей волны. Поэтому важно записать распределение амплитуды с высокой степенью контрастности, или вообще отделить плёнку, сохраняя запись фазы световой волны в толщине эмульсии. Другими словами, запись аналоговой информации по существу происходит в двоичном коде. При этом вовсе не важно, что считать за логическую единицу - максимальное почернение или максимальное осветление фотопластинки.
3. Третьим замечательным свойством таких динамических неоднородностей является большое число параллельных каналов записи информации выполняемых путём последовательного экспонирования. При этом аналоговая информация каждого информационного сигнала записывается на своей пространственной несущей частоте. В процессе восстановления волновых фронтов, содержащих динамические неоднородности, различные восстановленные волны будут распространяться по различным направлениям и локализоваться в определённых местах.
4. Четвёртым удивительным свойством записи аналоговой информации в виде голограммы является высокая помехозащищённость. Царапины, трещины, сколы и даже утрата части фотопластинки с "замороженными" динамическими неоднородностями световой волны не приведут к полной потере аналоговой информации. Это объясняется записью каждой точки объекта по всей поверхности голограммы.
5. Существует уникальное свойство голограмм. Это так называемая интерференция Наполеона с Клеопатрой. Смысл эффекта в следующем. Если на фотопластинку записать изображение предмета и, не проявляя её, через некоторое время снова записать текущее состояние того же предмета, то в результате взаимодействия двух изображений, разделенных промежутком времени, могут быть выявлены даже незначительные пространственные изменения предмета. Этот приём позволит исключить передачу повторяющихся массивов информации, а передавать только текущие изменения, разностную информацию.

Таким образом, форма записи информации в виде интерференционных картин предусматривает как аналоговую, так и цифровую обработку и оказывается более устойчивой, чем запись информации поэлементно.

Следует отметить, что интерференционный метод записи аналоговой информации может использовать любые волновые процессы: электромагнитные, акустические, статические и другие волны. Важно подобрать среды, в которых могут быть заморожены динамические неоднородности, на короткий или длинный интервал времени.

При записи информации в интерференционной форме процесс поиска нужной информации производится практически по всему объёму памяти одновременно, что способствует распараллеливанию обработки информации по многим каналам.

Куб памяти можно сформировать из щелочно-галоидного монокристалла с F-центрами. Световая волна подбирается такой интенсивности и длины волны, при которой происходит отбеливание F-центров.

Информационная ёмкость E оценивается величиной:

При N = 10¹⁵ см^-3 и = 10^-4 см значение E ~ 10¹³ бит. Оценки показывают, что вся накопленная и записанная человечеством информация равна 10¹⁵ бит, и для её записи требуется 2,4·10⁷ книг. Таким образом, для записи информации потребуется всего 100 кубиков памяти. Фейман показал, что для записи 1 бит информации достаточен кубик по 5 атомов на каждом ребре [2].

Проделаем эксперимент по одновременной записи двух предметов A и B на голограмму. Голограмма зафиксирует интерференционную картину объектов A и B. Лазерный пучок восстановит оба изображения A и B, что соответствует воспроизведению образа по отдельному фрагменту. Другими словами, речь идёт об ассоциативной памяти голограммы.

Это напоминает схему человеческого вспоминания образов, событий, текстов по отдельным частям, фрагментам. Был предложен ряд гипотетических механизмов накопления информации в мозге, основанный на взаимодействии распространяющихся волн. По-видимому, существует определённая аналогия между голограммой и ассоциативной памятью человека. Волновые процессы в мозге передаются ячейкам, которые изменяют свои свойства подобно процессу отбеливания F-центров в кубе памяти в когерентной волне. Причём можно представить такую систему нейронов в мозге, когда каждая ячейка одного слоя передаёт поступивший на неё электрический импульс возбуждения нерва к нескольким ячейкам следующего слоя нейронов. Этот способ позволяет накопить большое количество информации в весьма устойчивой форме. Важно соблюдать точные фазовые соотношения в волне на протяжении большого отрезка распространения сигнала.

Не исключено, что в мозге существует некоторая система, которая калибрует и компенсирует скорость распространения сигналов. Для устойчивости процесса поиска информации в схеме оптической ассоциативной памяти необходимо выделить две области.

В одной области памяти информация наблюдения и опыта смешивается для проведения быстрого поиска и распознавания (оперативная память). В другой области информация о различных ситуациях накапливается раздельно, хранится достаточно долго (постоянная память). При этом происходит обмен информацией между обеими областями памяти [10].

Отметим, что в рамках современного воззрения на мозг различают также два вида памяти: кратковременную и долговременную. Чем не ОЗУ или ПЗУ!

В литературе ещё не встречалось понятия бита в голографических методах обработки информации, в биологических системах, тем более, в процессе обработки информации человеческим мозгом. В последние десятилетия специалистами овладела идея использовать квантовые системы в вычислительных устройствах. В этом случае в качестве единицы информации используется уже не бит, а новая величина - кубит.

Видимо, мы стоим на пороге второй революции в процессах обработки и хранения информации, в основе которой лежит дополнение идей классической теории информации идеями квантовой механики.

Квантовые вычисления и квантовые вычислительные системы

В классических схемотехнических компьютерах элементы логики и элементы памяти имеют только 2 состояния - "1" или "0". В этом случае, если состояние занято с вероятностью P(0)=1 и P(1)=0, то имеем булево логическое состояние "0", а если вероятность P(0)=0 P(1)=1, то логическое состояние "1".

Умышленно опустим случай многозначной логики в схемотехнических вычислительных устройствах и многобитовое представление информации в устройствах функциональной электроники.

Неразрешимые проблемы классической теории информации завтра надеются решить с помощью квантовой теории информации.

Элементарной единицей в квантовой теории информации является кубит. Он был введён в 1995 году Шумахером [12]. Один кубит информации рассматривается как система с двумя состояниями.

Два ортогональных состояния одного кубита записываются как

Для более общего случая 2ⁿ ортогональных состояний можно записать

где i - n-битовое двоичное число. Например, для случая трёх кубитов имеем:

Простые унитарные операции над кубитами называют квантовыми логическими гейтами. Приведём простейшие примеры элементарных квантовых гейтов:

• эквивалентность определяется как ;
• 

Анализ физики работы квантово-механических устройств и систем показывает, что в природе существует множество систем с двумя уровневыми состояниями: направление спина частицы, вектор поляризации света, двухуровневая квантовая система и так далее [2,13].

Однако есть важная физическая особенность таких систем.

Например, в случае поляризации фотонов есть два состояния, представляющих собой суперпозицию кубитов.:

и

Эти состояния соответствуют направлению поляризации света под углом ±45º.

В общем виде имеется суперпозиция базисных состояний:

где a и b - комплексные амплитуды состояний, такие что ||² + |ß|² = 1.

Вклад базисных состояний и характеризует вероятности P(0) = ||² и P(1) = |ß|².

В квантовых вычислительных системах состояние кубита характеризуется также когерентными или интерференционными слагаемыми, определяемыми произведениями комплексных амплитуд ²*ß и ²ß*.

Таким образом, состояние квантовой вычислительной системы, в отличие от классической, может меняться не только за счёт вероятностей P(0) и P(1), но и путём изменения амплитуд состояний и ß.

В этом случае говорят о повороте вектора состояний в двумерном пространстве, в математике называемым гильбертовым пространством.

Суперпозиция состояний системы из k кубитов характеризуется 2^k комплексными числами и увеличивает размерность гильбертова пространства до 2^k и, соответственно, числа интерференционных составляющих.

В теории квантовых систем существует функциональное понятие "запутанное состояние". Для пары кубитов такое состояние характеризуется, например, состоянием:

В этом случае ни один из кубитов не находится в определённом состоянии.

В квантовой системе кубиты находятся в состоянии линейной суперпозиции с комплексными коэффициентами. Квантовый вычислительный процесс или процессинг представляется как набор унитарных преобразований, действующих на набор суперпозиций.

При обработке информации квантовыми вычислительными структурами открываются принципиально новые свойства информации:

• суперпозиция: вычисления представляют собой унитарное преобразование когерентных квантовых состояний;
• интерференция: параллельные пути вычисления, в зависимости от набега фазы, могут приводить либо к усилению, либо к ослаблению (вплоть до уничтожения) соответствующей амплитуды;
• запутанность: некоторые состояния квантовой системы могут не распадаться в произведение состояния её частей;
• неопределённость и неконтролируемость информации: известное квантовое состояние не может быть точно скопировано (клонировано) и подвергнуто наблюдению (считыванию) без риска разрушения.

Идея создания квантового компьютера основывается на выполнении квантового алгоритма вычислений, представляющего собой определённое число однокубитовых и двухкубитовых операций. Основной частью квантового компьютера является квантовый регистр (рис. 6).

Рисунок 6. Структура квантового компьютера

Квантовый регистр представляет собой совокупность L кубитов. Все кубиты регистра перед началом вычислений должны быть приведены в основные базисные (булевы) состояния. Другими словами,

Такая операция называется инициализацией.

Одним из заданных физических процессов, который обязательно для надёжности должен управляться классическим компьютером, заключается в том, что каждый кубит подвергается селективному воздействию. В этом случае кубит будет трансформирован по схеме:

Состояние всего регистра перейдёт в суперпозицию базисных состояний вида

где n_i = 0,1... - задающее базисное представление числа

Состояние регистра с помощью соответствующих физических импульсных воздействий преобразуется в соответствующую когерентную суперпозицию базисных состояний по правилу:

Эта суперпозиция попадает в процессор, выполняющий унитарные преобразования U(t), представляющие собой квантовые логические операции.

На выходе процессора возникает новая суперпозиция вида:

Роль программного обеспечения подготовки информации для ввода в процессор играет совокупность возможных операций на входе, формирование исходных состояний, формирование импульсов воздействия на кубиты, осуществление декогерентизации квантовых состояний, исправление случайных ошибок.

В качестве элементной базы квантовых компьютеров могут быть использованы следующие квантовые системы:

• ионы, захваченные ионными ловушками, создаваемыми в вакууме определённой конфигурацией электрического поля при их глубоком охлаждении;
• атомы с ядерными спинами с I= 1/2, принадлежащие молекулам органических жидкостей, со скалярным взаимодействием между ними и методы ядерного магнитного резонанса (ЯМР) для управления кубитами;
• зарядовое состояние куперовских пар в квантовых точках, связанных с переходами Джозефсона;
• твердотельный ядерный магнитный резонанс атомов 31P, имплантированных в кремниевую структуру и обладающих спинами 1/2. Система работает при низких температурах и достаточно сильных магнитных полях;
• два зарядовых электронных состояния в полупроводниковых наноструктурах типа AlGaAs/GaAs со спиновым электрическим взаимодействием между кубитами;
• квантовые точки с электронными зарядовыми (орбитальными) состояниями, с электронными спинами в электродинамическом резонаторе, с несколькими электронными и одним ядерным спином.

Заключение

В новое тысячелетие мир входит с идеей квантовых вычислений с гипотетическими конструкциями квантовых компьютеров. Надо сразу заметить, что квантовые вычисления не скоро заменят классические, если вообще это когда-то произойдёт.

На сегодняшний день констатируем, что:

• не ясна суть квантовых вычислений;
• не определён общий класс вычислительных задач, для которых можно найти эффективные решения;
• неизвестно, можно ли достичь значительной вычислительной мощности, используя менее 100 кубит;
• неизвестны законы природы в области информации и квантовой механики, схожие с законами сохранения в классической физике…

Когда же будут созданы мощные квантовые компьютеры, они будут использованы только для класса задач, решение которых более эффективно с точки зрения квантовой информатики.

Литература

1. Советский энциклопедический словарь. М, 1983.
2. Кадомцев Б.Б. Динамика и информация. М.: Редакция журнала "Успехи физических наук", 1997.
3. Shannon C.E. The redundancy of English. In: Cybernetics. Transactions of the 7th Conference. New York, 1951.
4. Винер Н. Кибернетика, или управление и связь в животном и машине. М.: Советское радио, 1958.
5. Степаненко И.П. Основы микроэлектроники. М.: Лаборатория базовых знаний, 2000.
6. Лихарев К.К. О возможности создания аналоговых и цифровых интегральных схем на основе дискретного туннелирования. Микроэлектроника. 1987. Т. 16. вып. 3. с. 195.
7. Драгулов В.П., Неизвестный И.Г., Гридчин В.А. Основы наноэлектроники. Новосибирск, 2000.
8. Галушкин А.И. Нейрокомпьютеры и их применение. М.: Радиотехника, 2000.
9. Захарченко, А.А. Щука Развитие оптических нейрокомпьютеров. Электронная промышленность М.: ЦНИИ Электроника. 2001. № 5.
10. Щука А.А. Функциональная электроника. М.: МИРЭА, 1998.
11. Прибрам К. Языки мозга. М.: Прогресс, 1975.
12. Schumacher B. Quantum coding. Phys. Rev. A 51 1995. P. 2738–2747.
13. Валиев К.А., Кокин А.А. Квантовые компьютеры: надежда и реальность. Ижевск: НИЦ Регулярная и хаотическая динамика, 2001.