Н. Семенов
MATLAB для DSP. Моделирование приемника DTMF. Часть 1
Введение
Настоящая статья — очередная публикация в рамках проекта “MATLAB для DSP”, посвящена важнейшему инструменту пакета MATLAB — средству имитационного моделирования Simulink. Как и в предыдущей публикации, мы рассмотрим конкретный пример, и обсудим особенности применения Simulink.
Пример связан с проектированием очень распространённого в средствах телефонии прибора — приёмника тонального вызова DTMF. Реализуемый средствами цифровой обработки сигналов (обычно на ЦПОС) приёмник должен удовлетворять жёстким требованиям стандарта и при этом быть предельно экономным по производительности и затратам памяти. Не случайно по этой причине в литературе обсуждаются различные варианты алгоритмов DTMF и способы их реализации. Мы рассмотрим одно из новых предложений по данному вопросу.
После краткого изложения рекомендации по DTMF и нового алгоритма в статье приводится функциональная схема приёмника. По ней из библиотеки Simulink выбираются функциональные блоки, необходимые для построения модели, и определяются их параметры. Затем проводится первый этап моделирования, после чего вносятся необходимые коррекции. Моделирование и коррекции осуществляются до тех пор, пока на стандартном тестовом материале не получатся необходимые результаты.
Следует особо подчеркнуть, что финальная модель является достаточной для построения реальных приёмников DTMF.
Описание моделируемой системы
Практическая задача приёма DTMF очень часто становится актуальной в задачах телекоммуникации, так как сигнал DTMF является пока единственным средством надёжной доставки информации от конечного пользователя через аналоговую телекоммуникационную сеть до устройства обработки. Сам сигнал DTMF является суммой отрезков двух гармонических колебаний, частоты которых соответствуют номеру строки и столбцу цифры номеронабирателя обычного телефона. Соответствие частот номерам строк и колонок показано на рис. 1.
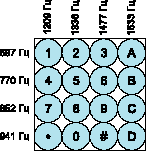
Рис. 1. Соответствие частот и символов
Для уверенного приёма такого сигнала на сам сигнал и на его приёмник накладываются ограничения, определённые в спецификациях ITU-T (таблица).
Таблица
| Точность генерации частоты |
Принимать при отклонении меньше 1,5%. Не принимать при отклонении больше 3% |
| Длительность сигнала |
Принимать сигнал длиннее 40 мс. Не принимать сигнал короче 23 мс. |
| Разрывы сигнала |
Сигнал DTMF, прерванный паузой < 10 мс, считать одним символом |
| Пауза между сигналами |
Пауза не менее 40 мс является разделителем между двумя сигналами DTMF |
| Амплитуда сигнала |
Наименьшая амплитуда сигнала, которую должен детектировать приемник, -26 дБм |
| Соотношение сигнал/шум |
Наихудшее соотношение сигнал/шум - 15 дБ |
| Твист |
Приемник должен работать при прямом твисте 8 дб и обратном - 4 дб. (Твистом называется разница между амплитудами двух основных частот сигнала DTMF) |
| Срабатывание на человеческую речь |
Приемник должен нормально функционировать в присутствии речи без ложных срабатываний |
В данной статье обсуждается новый алгоритм приёма DTMF, построенный на подсчёте периода сигнала с использованием переходов через “ноль”. Так как DTMF состоит из двух гармонических сигналов, обработка сводится к разделению этих сигналов и оценки частоты каждого из них. Имея оценку частоты каждого из двух гармонических сигналов, можно установить допустимые границы частоты искомого сигнала. Функциональная схема такого устройства представлена на рис. 2.
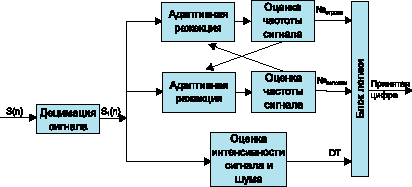
Рис. 2. Функциональная схема приемника DTMF
Сначала происходит децимация сигнала с 8 до 4 кГц (блок “Децимация сигнала”). Это снижает дисперсию шума на 1/ 2, что позволяет увеличить эффективный динамический диапазон. Далее полученный сигнал подаётся на два режекторных фильтра (блоки “Адаптивная режекция”) и на блок оценки интенсивности сигнала. Передаточные функции режекторных фильтров имеют следующий вид:
H(z) = 1 - cos(2 * p * f3/4000) * z-1 + z-2
Нули передаточной функции расположены на единичной окружности. При такой форме H(z) легко менять параметры фильтра с помощью одного коэффициента. Режекторные фильтры позволяют вырезать узкую полосу частот. Если сигнал есть сумма отрезков двух гармонических колебаний, их можно разделить по двум ветвям алгоритма и оценить частоту каждого, вычислив их периоды, используя принцип перехода через “ноль”. Для практической реализации удобно рассматривать период сигнала как число целых интервалов дискретизации за один период сигнала плюс дробная часть, получаемая при линейной интерполяции сигнала между двумя отсчётами (рис. 3).
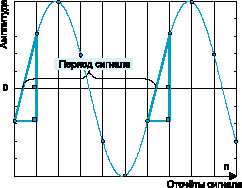
Рис. 3. Дискретизация сигнала
В случае попадания этой частоты в один из заданных интервалов в одном из каналов, происходит перерасчёт параметров режекторного фильтра в другом канале. Таким образом система из двух режекторных фильтров придет в устойчивое состояние только тогда, когда в каждой ветви из сигнала останется только по одной гармонической составляющей.
Блок оценки интенсивности сигнала отвечает за принятие решения, есть ли в данный момент резкий скачок интенсивности сигнала или нет. При SNR = 15 дБ и более такой скачок при приходе очередной цифры DTMF можно легко выделить, сравнивая интенсивность сигнала с порогом срабатывания. Для оценки интенсивности используется сглаживающий фильтр, уравнение “вход-выход” которого имеет следующий вид:
y(n) = a * y(n - 1) + (1 - a) * |s(n)|,
где y(n) — сигнал на выходе фильтра, а s(n) — входной сигнал. Параметр a берётся равным 0,95.
Логический блок принимает решение о наличии новой цифры и обеспечивает соответствие приёма спецификации ITU-T.
Принцип его работы следующий: если блок оценки интенсивности определил наличие сигнала и цифра, определившаяся после оценки частоты двух компонент сигнала, не меняются в течение 5 мс, начинается вычисление длительности сигнала цифры. Если после этого сигнал пропадёт на время, меньше 10 мс, то подсчёт времени сигнала продолжается после его восстановления. Принятой считается цифра, суммарная длительность которой не менее 23 мс, и после которой была пауза более 10 мс.
Моделирование функциональных блоков
Построение блок-схемы модели
Для более полного соответствия модели описанному выше приёмнику DTMF, удобно создавать модель в виде той же блок-схемы, что и в описании приёмника, а затем заполнять эти блоки необходимым содержимым. Пакет Simulink содержит в своей библиотеке всё необходимое для этого:
Блок подсистемы
При двойном щелчке мышью на этом блоке происходит открытие нового окна подсистемы. Но, как видно из изображения блока, у него нет ни входов, ни выходов. Для того, чтобы добавить их, необходимо вставить в каждую подсистему соответствующие блоки входов и выходов, а также назвать их удобными для понимания именами. Подробное описание работы со стандартными блоками пакета Simulink было описано в [4].
Входы и выходы подсистемы
Если в подсистему вставить нужное количество входов и выходов, то они тут же появятся и на изображении блока подсистемы.
На основании вышеизложенного можно построить “скелет” будущей модели, показанный на рис. 4.
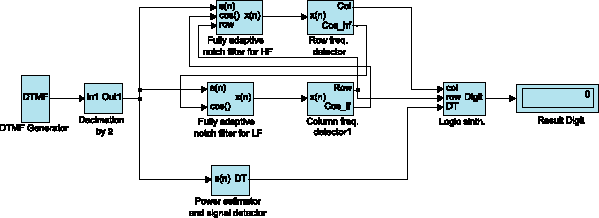
Рис. 4. Блок-схема модуля DTMF-приемника
Все блоки этой модели соответствуют блокам структурной схемы приёмника DTMF, показанной на рис. 2, и даже расположены в соответствии с ней. Дополнительными элементами являются только источник сигнала и индикатор принятой цифры. Для подтверждения авторских прав и автоматического хранения даты последней модификации можно воспользоваться соответствующим блоком из пакета Simulink.
Заполнение блока “DTMF Generator”
Для удобства моделирования полезно сделать этот блок таким, чтобы можно было:
- генерировать сигнал с заданными свойствами;
- брать сигнал из файла;
- брать сигнал из рабочей области MATLAB.
Для этого потребуются следующие стандартные блоки пакета Simulink.
Блок считывания сигнала из файла
Файл, имя которого указано в виде параметра, должен быть файлом данных в формате системы MATLAB.
Этот блок позволяет считывать данные прямо из mat-файла, что очень удобно для тестирования системы на реальных данных. Для настройки блока достаточно дважды щёлкнуть по нему левой клавишей мыши, после чего появится следующее диалоговое окно, показанное на рис. 5.
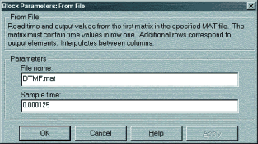
Рис. 5
Как видно на рис. 6, в первой строке ввода нужно ввести имя файла, из которого будут считываться данные, а во второй — интервал времени между отсчётами сигнала.
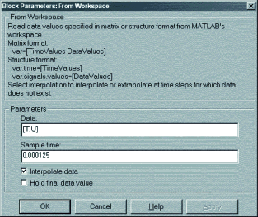
Рис. 6
Блок считывания сигнала из рабочей области MATLAB
Этот блок предназначен для использования данных, находящихся в рабочей области MATLAB, то есть уже загруженных в память.
Настройка блока (рис. 6) состоит из следующих полей:
- имя переменной, в которой есть данные о времени и значении сигнала;
- интервал дискретизации;
- флажок, выставляемый при необходимости интерполировать данные, если временные метки в переменной и модели не совпадают;
- флажок, выставляемый при необходимости удерживать последнее значение после окончания данных.
Блок генератора сигналов
Этот блок позволяет генерировать синусоидальный сигнал, меандр или пилообразный сигнал и позволяет задавать частоту в Гц (рис. 7).
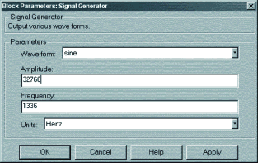
Рис. 7
Блок генератора белого шума
Генератор белого шума, спектр которого ограничен половиной частоты дискретизации, позволяет моделировать шумовую компоненту сигнала.
В качестве параметров шума задаётся мощность процесса, интервал дискретизации и инициирующее значение для генератора случайных чисел (рис. 8).
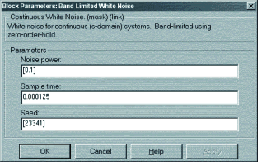
Рис. 8
Мультиплексор
Позволяет переключать несколько входных устройств на одно выходное по определённому правилу.
Единственный параметр, необходимый для работы мультиплексора — количество переключаемых входов (рис. 9).
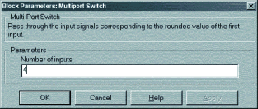
Рис. 9
В нашем случае, число переключаемых входов равно 4, а верхний вход является управляющим. На него должно быть подано целое число, определяющее номер входа, который в данный момент должен быть подключен к выходу.
Генератор заданной повторяющейся последовательности
Он нужен для определения, в какой момент времени какой из генераторов будет использоваться.
В качестве параметров задаются временные метки и значения сигнала в них (рис. 10).
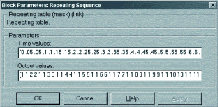
Рис. 10
При заданных значениях параметров на выходе этого блока получается результат (который для удобства пользователя также виден и на графическом изображении блока), показанный на рис. 11.
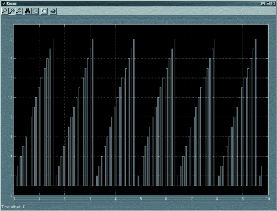
Рис. 11. Осциллограмма на выходе генератора повторяющейся последовательности
Сначала реализуем генерацию всех цифр DTMF с помощью генераторов, как это показано на рис. 12.
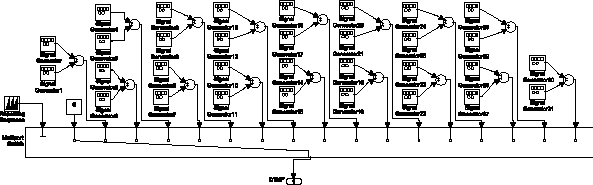
Рис. 12. Генератор цифр DTMF
Здесь с помощью мультиплексора, имеющего 17 входов (16 цифр + пауза), происходит передача одной из цифр или паузы на выходной порт DTMF. Этим процессом управляет генератор заданной последовательности, в параметрах которого задано время переключения и значение, которое нужно в это время удерживать.
На основании вышеизложенного, построим универсальный генератор сигнала, который генерирует сигнал с заданными параметрами, смешивает его с шумовым процессом заданной мощности, позволяет брать сигнал из файла или из рабочей области MATLAB. Пример такого блока показан на рис. 13. На нём для увеличения наглядности всё то, что было на рис. 12, собрано в виде подблока. Чтобы сделать подблок, нужно выделить с помощью мыши нужный фрагмент, а затем в меню “Edit” выбрать “Create Subsystem” или нажать “Ctrl-G”. Альтернативным вариантом является создание подсистем, как это было показано при построении блок-схемы модели.
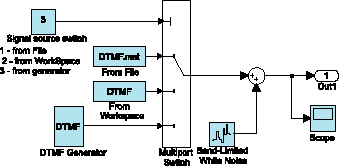
Рис. 13. Универсальный генератор сигналов
Для выбора способа генерации сигнала достаточно изменить значение константы, подаваемой на верхний (управляющий) вход мультиплексора, тогда на его выход попадёт сигнал с входа, номер которого соответствует значению константы. Как видно из рис. 13, запись константы “1” приведёт к воспроизведению сигнала из файла; запись константы “2” — сигнала из памяти MATLAB, если кто-то загрузил туда эти данные; и запись “3” — получение сигнала DTMF с помощью настраиваемых генераторов. Для подмешивания шума в сигнал нужно изменить параметры генератора шума, сделав ненулевой его мощность. Чтобы увидеть осциллограмму сигнала на выходе Out1, достаточно дважды щёлкнуть мышью на блоке осциллографа, чтобы на экране появилось окошко с экраном осцилло-графа, и запустить симуляцию. При этом на экране осциллографа при выбранных параметрах будет сигнал, показанный на рис. 14.
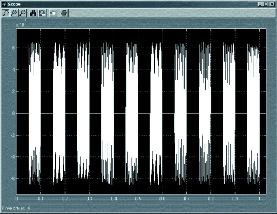
Рис. 14. Осциллограмма сигнала на выходе Out1
Заполнение блока “Decimation by 2”
Этот блок — блок децимации сигнала. Для его реализации можно воспользоваться готовым блоком цифрового фильтра.
Для настройки этого блока необходимо задать коэффициенты передаточной функции фильтра (числителя и знаменателя) и интервал дискретизации (рис. 15).
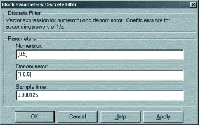
Рис. 15
Для наглядности удобно воспользоваться стандартной формой представления фильтра, изображённой на рис. 16.
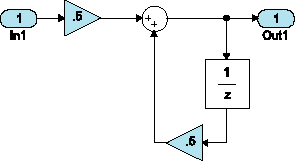
Рис. 16
Новых блоков здесь два: единичная задержка, описываемая только интервалом дискретизации, и коэффициент усиления, показывающий, насколько изменится амплитуда сигнала при прохождении данного блока. Оба коэффициента усиления на блоке равны 0,5. В свойствах входного блока (“In1”) установлен интервал дискретизации 0,000125 мкс, такой же интервал указан и в параметрах блока единичной задержки (“1/z”).
Литература
- Дьяконов В.П., Абраменков И.В. MATLAB 5.0/5.3. — М.: Нолидж. — 1999. — 633 с.
- Гультяев А.К. Имитационное моделирование в среде Windows. — СПб.: КОРОНА принт. — 1999. — 288 с.
- Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования. 2-е изд., доп. — СПб.: БГТУ. — 1996. — 191 с.
- Анохин В.В. MATLAB для DSP. Моделирование аналого-цифрового преобразования // Chip News. — 2000. — № 2. — С. 3–7. — № 3. — С. 26–29.
- Amey A. Deosthali, Shawn R. McCaslin, Brian L. Evans, A Low-Complexity ITU-Compliant Dual Tone Multiple Frequency Detector, draft, http://signal.ece.utexas.edu/.
E-mail: nick@rts.loniis.ru
|